AA 树
AA 树是一种用于高效存储和检索有序数据的平衡树形结构,Arne Andersson 教授于 1993 年在他的论文 "Balanced search trees made simple" 中介绍,设计的目的是减少红黑树考虑的不同情况。AA 树可以在
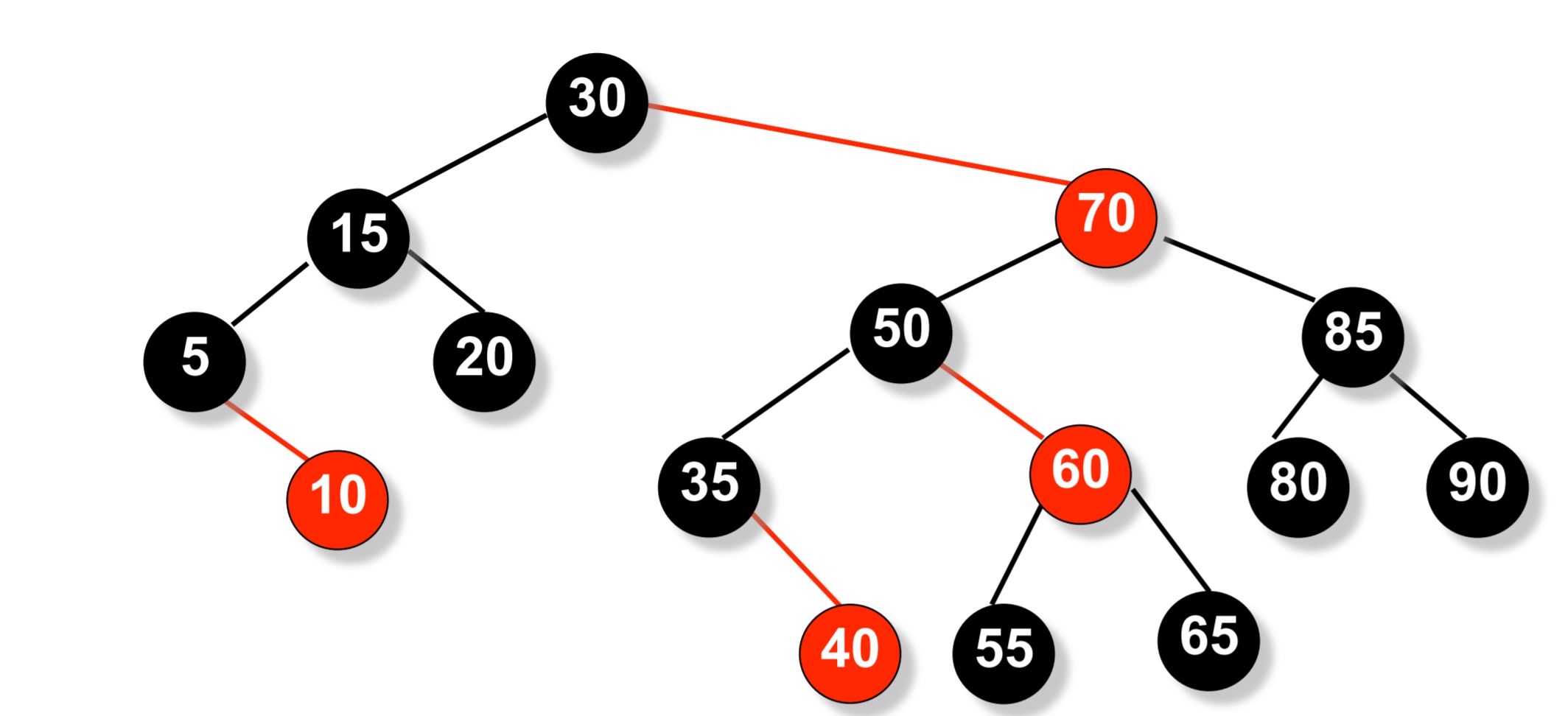
AA 树是红黑树的一种变体,与红黑树不同,AA 树上的红色节点只能作为右子节点。这导致 AA 树模拟了 2-3 树而不是 2-3-4 树,从而极大地简化了维护操作。红黑树的维护算法需要考虑七种不同的情况来正确平衡树。
因为红色节点只能作为右子节点,AA 树只需要考虑两种情况。
定义
AA 树遵循与红黑树相同的规则,但添加了一条新规则,即红色节点不能作为左孩子出现。
- 每个节点都可以是红色或黑色。
- 根节点总是黑色。
- 叶节点(NULL)总是黑色。
- 红色节点的两个子节点必须都是黑色,即没有两个相邻的红色节点。
- 从根节点到 NULL 节点的每条路径都有相同数量的黑色节点。
- 红色节点只能作为右子节点。
平衡维护
AA 树的每个节点维护一个 level 字段,类似红黑树的每个节点维护一个 color 字段 ("RED" or "BLACK")。level 的规定满足以下 5 个条件:
1、每个叶节点的 level 是 1。
2、每个左孩子的 level 是其父节点的 level 减 1。
3、每个右孩子的 level 等于其父节点的 level 或等于其父节点的 level 减 1。
4、每个右孙子的 level 严格小于其祖父节点的 level。
5、每个 level 大于 1 的节点有两个孩子。
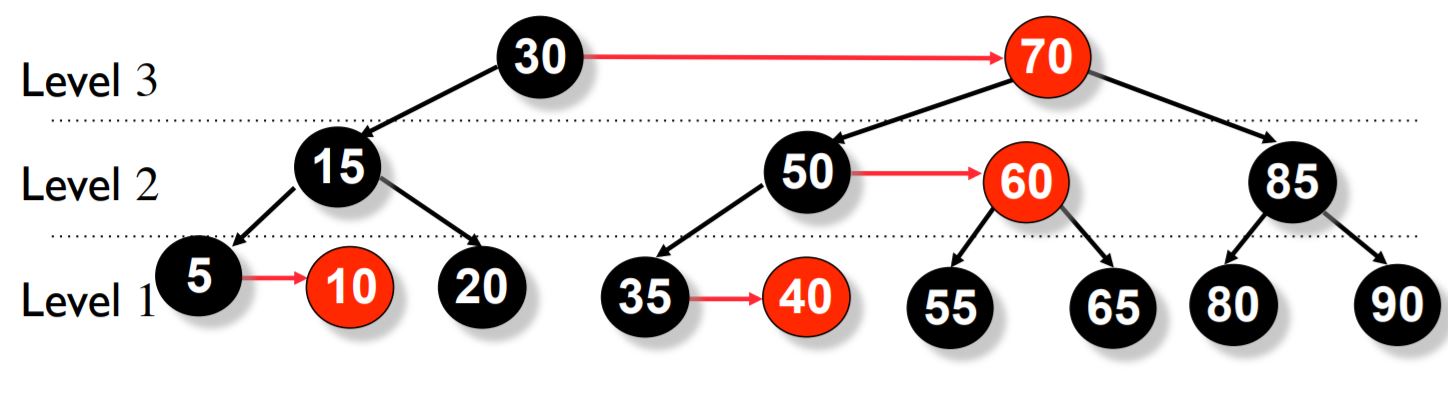
水平链接(Horizontal Link)
子节点的 level 等于父节点的 level 的链接被称为 水平链接,类似于红黑树中的红链接。允许单独的右水平链接,但不允许连续的右水平链接;不允许左水平链接。这些限制比红黑树的限制更加严格,因此 AA 树的平衡过程比红黑树的平衡过程在程序上要简单得多。
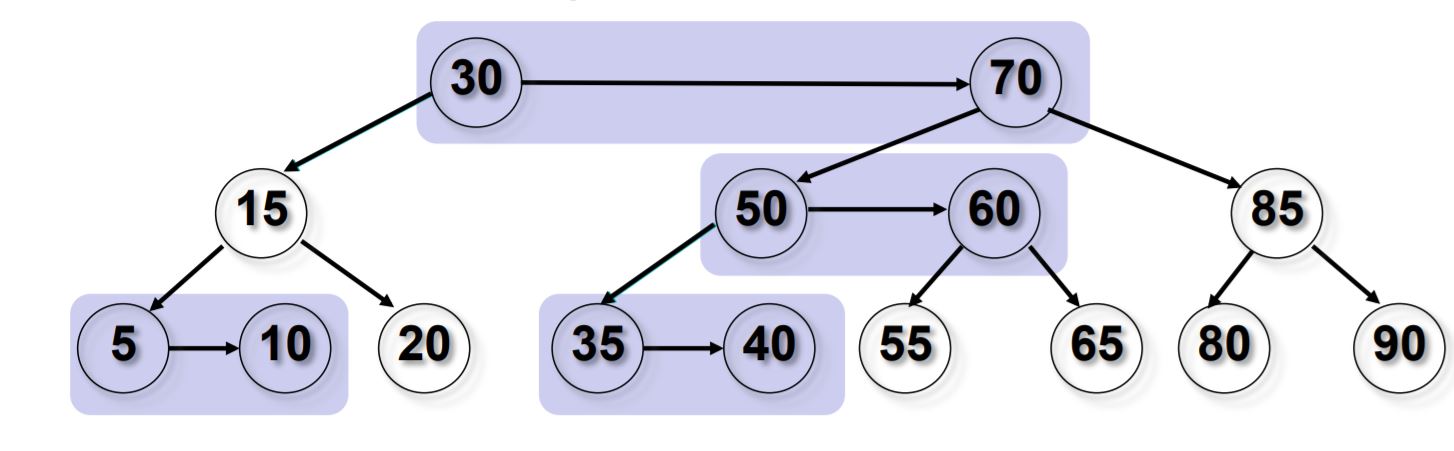
插入和删除操作可能会暂时导致 AA 树失去平衡(即违反 AA 树的不变性)。恢复平衡只需要两种不同的操作:"skew"(斜化)和"split"(分裂)。"Skew"是将一个包含左水平链接的子树进行右旋转,以替换为一个包含右水平链接的子树。"Split"是进行左旋转并增加 level,以替换一个包含两个或更多连续的右水平链接的子树,使其变为一个包含两个较少连续的右水平链接的子树。保持平衡的插入和删除的实现通过依赖"skew"和"split"操作来仅在需要时修改树,而不是由调用者决定是否进行"skew"或"split",从而变得更加简化。
split(左旋)
出现连续向右的水平方向链(连续三个向右的孩子属于同一 level,节点 R 和节点 X 都是红色节点)。
此时向左旋转节点T,把小于等于此 level 的节点看做一个子树。
- 子树的根的右孩子变为新的子树根;
- 原来的子树根变为新子树根的左孩子;
- 新的子树根 level+1。
伪代码实现
skew(右旋)
出现向左的水平方向链(连续两个向左的孩子属于同一 level)
向右旋转节点T,把小于等于此 level 的节点看做一个子树。
- 子树的根的左孩子变为新的子树根;
- 原来的子树根变为新子树根的右孩子。
伪代码实现
AA 树的操作
AA 树本身是一棵二叉搜索树,所以搜索操作与其他二叉搜索树相同。插入和删除操作与AVL树相同,首先在树中将 key 插入或删除,然后沿着搜索路径回退到根,并在此过程中重构树。
插入
伪代码实现
删除
删除过程与其他二叉平衡树类似,首先将内部节点的删除转换为叶子节点的删除。具体方法是将内部节点与它最接近的前驱或后继节点替换。由于 AA 树的所有 level 大于 1 的节点都有两个子节点,前驱或后继节点将位于 level 1,删除 level 1 的节点较为简单。
伪代码实现
性能
AA 树的性能与红黑树的性能相当。尽管 AA 树进行的旋转操作比红黑树多,但 AA 树的算法更简单,最终导致相近的性能。红黑树的性能在各种情况下更加一致,而 AA 树往往更扁平,这使 AA 树有稍快的搜索速度。
参考资料
- AA tree - Wikipedia
- Introduction to AA trees
- AA tree - Visualization
- CMSC 420 Lecture 6: 2-3, Red-black, and AA trees
本页面最近更新:2024/8/4 21:20:39,更新历史
发现错误?想一起完善? 在 GitHub 上编辑此页!
本页面贡献者:c8ef, yuhuoji
本页面的全部内容在 CC BY-SA 4.0 和 SATA 协议之条款下提供,附加条款亦可能应用



